AC CIRCUIT

AC Circuits :. 
                            Prerequisites:
  An  alternating  current  (AC)  is  an  electrical  current,  where  the  magnitude  of  the current  varies  in  a  cyclical  form,  as  opposed  to  direct  current,  where  the  polarity  of  the  current stays  constant.


The usual  waveform  of  an  AC  circuit  is  generally  that  of  a  sine  wave,  as  this  results  in the  most  efficient  transmission  of  energy.  However  in  certain  applications  different  waveforms are  used,  such  as  triangular  or  square  waves.


Introduction :
 Used  generically,  AC  refers  to  the  form  in  which  electricity  is  delivered  to  businesses and  residences.  However,  audio  and  radio  signals  carried  on  electrical  wire  are  also  examples of  alternating  current.  In  these  applications,  an  important  goal  is  often  the  recovery  of information  encoded  (or  modulated)  onto the  AC  signal.

 Kirchhoff’s  law: Kirchhoff's  Current  Law: First  law  (Current  law  or  Point  law): Statement: The  sum  of  the  currents  flowing  towards  any  junction  in  an  electric  circuit  equal  to  the  sum  of currents flowing  away  from  the junction. 


 Kirchhoff's  Current  law  can  be  stated  in  words  as  the  sum  of  all  currents flowing  into  a  node  is  zero.  Or  conversely,  the  sum  of  all  currents  leaving  a  node  must be  zero.  As  the  image  below  demonstrates,  the  sum  of  currents  Ib,  Ic,  and  Id,  must equal  the  total  current  in  Ia.  Current  flows  through  wires  much  like  water  flows through  pipes.  If  you  have  a  definite  amount  of  water  entering  a  closed  pipe  system, the  amount  of  water  that  enters  the  system  must  equal  the  amount  of  water  that exists  the  system.  The  number  of  branching  pipes  does  not  change  the  net  volume  of water  (or  current  in our  case)  in  the  system.
   

Kirchhoff's  Voltage  Law: Second  law  (voltage  law  or  Mesh  law):  

Statement:

 In  any  closed  circuit  or  mesh,  the  algebraic  sum  of  all  the  electromotive  forces  and  the voltage  drops  is  equal  to  zero.  

 Kirchhoff's  voltage  law  can  be  stated  in  words  as  the  sum  of  all  voltage  drops  and  rises  in a  closed  loop  equals  zero.  As  the  image  below  demonstrates,  loop  1  and  loop  2  are  both  closed loops  within  the  circuit.  The  sum  of  all  voltage  drops  and  rises  around  loop  1  equals  zero,  and the  sum  of  all  voltage  drops  and  rises  in  loop  2  must  also  equal  zero.  A  closed  loop  can  be defined  as  any  path  in  which  the  originating  point  in  the  loop  is  also  the  ending  point  for  the loop.  No  matter  how  the  loop  is  defined  or  drawn,  the  sum  of  the  voltages  in  the  loop  must  be zero .

   The sum of all the voltages around a loop is equal to zero.                                V1 + v₂ + v₃ +v₄ = 0

Steady State  Solution of DC Circuits: Resistance  in  series  connection:

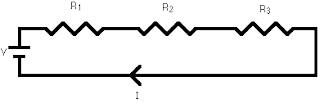
The resistors  R1,  R2,  R3  are  connected  in  series  across  the  supply  voltage  “V”.  The  total  current flowing  through  the  circuit  is  denoted  as  “I”.  The  voltage  across  the  resistor  R1, R2  and  R3  is  V1, V2, and V3  respectively. 

  V1  =  I*R1  (as per ohms law) 

V2.   =  I*R2

 V3   =  I*R3

 V     =  V1+V2+V3 

         =  IR1+IR2+IR3 

          =  (R1+R2+R3) I 

 IR.      =  (R1+R2+R3)

  R.       = R1+R2+R3

 Resistance  in  parallel connection:  

The  resistors  R1,  R2,  R3  are  connected  in  parallel  across  the  supply  voltage  “V”.  The  total current  flowing  through  the  circuit  is  denoted  as  “I”.  The  current  flowing  through  the  resistor R1, R2  and R3  is  I1,  I2, and  I3  respectively.   

                     I  =  V / R  (as  per  ohms  law)

                     I1  =  V1  / R1 

                     I2  =  V2  / R2 

                     I3 =  V3  / R3 

         V 1 = V2  =  V3  =  V  From the above  diagram  

                      I  =  I1+I2+I3 

                         =  V1  / R1  +  V2  /  R2  +  V3  / R3 

                         =  V / R1+  V/R2  +V/R3

                    I    = V (1/R1  +1/R2  +1/R3) 

              V / R  =  V (1/R1  +1/R2  +1/R3) 

                 1/R = 1/R1  +1/R2  +1/R3